Penulis: Nikolas Putra Hadianto (2511030)
Dalam mekanika bahan, kita belajar mengenai uji tarik yang berakhir pada kegagalan fraktur. Lalu bagaimana dengan kolom yang mengalami tekanan? Jika kolom dianggap memiliki bentuk yang sempurna serta beban yang tepat berada di tengah permukaan kolom, tekanan berlebih akan membuat kolom tersebut hancur. Namun, pada kenyataannya tidak ada kolom dan pembebanan yang sempurna (tepat berada di tengah permukaan). Akibatnya, alih – alih hancur, kolom yang mengalami beban kompresif berlebih akan tertekuk ke arah lateral.
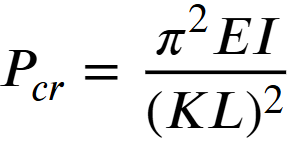
Gambar 1. Euler’s Critical Load Formula
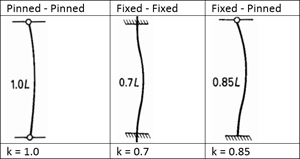
Gambar 2. Panjang Efektif Kolom
Untuk memahami konsep tekuk khususnya pada kolom baja secara matematis, kita perlu memahami persamaan beban tekuk elastis (gambar 1). Pcr adalah beban kritis yang menunjukkan stabilitas struktur ketika diberikan beban dengan nilai tertentu.
- Jika P < Pcr, kolom berada pada keseimbangan stabil.
- Jika P = Pcr, kolom berada pada keseimbangan netral.
- Jika P > Pcr, kolom berada pada keseimbangan tidak stabil—gangguan kecil saja dapat menyebabkan deformasi yang signifikan.
Berdasarkan persamaan tersebut, terdapat beberapa variabel yang dapat mempengaruhi tekuk pada kolom :
1. Modulus Elastisitas (Elastic Modulus)
Dalam kasus tekuk pada kolom, modulus elastisitas menunjukkan ketahanan material terhadap tekuk. Semakin besar modulus elastisitas semakin kuat material menahan tekuk yang terjadi. Dalam hal ini, baja umumnya memiliki nilai E sebesar 200 GPa. Nilai tersebut cukup besar bila dibandingkan dengan material lain sehingga baja bersifat lebih kaku dalam menahan tekuk.
2. Inersia Momen Area (Second Moment of Inertia)
Berbeda dengan modulus elastis, inersia momen area menunjukkan kekakuan geometris dari kolom. Variabel ini juga berbanding lurus dengan beban tekuk kritis. Artinya, semakin besar nilai I, semakin besar pula beban kompresi yang dapat diterima kolom tanpa mengalami tekuk.
3. Panjang Kolom Sebenarnya (L)
Panjang sebuah kolom juga menjadi hal yang krusial dalam pembebanan kompresif. Berdasarkan persamaan tersebut, kita mengetahui bahwa beban kritis berbanding terbalik dengan kuadrat panjang kolom. Hal ini menunjukkan kolom yang lebih panjang akan menurunkan beban kritis secara drastis sehingga kolom akan rentan mengalami tekuk.
4. Faktor Panjang Efektif (K)
Nilai variabel K berbeda tergantung pada sambungan di ujung kolom (gambar b). Kolom dengan sambungan jepit-bebas akan memiliki nilai K yang lebih besar, sedangkan kolom dengan sambungan jepit-jepit akan memiliki nilai K yang lebih kecil. Sama seperti variabel L, faktor panjang efektif juga berbanding terbalik dengan beban kritis yang membuat K dengan nilai yang lebih kecil (sambungan jepit-jepit) akan lebih kaku dalam menahan tekuk pada kolom.
Dari persamaan tersebut, kita mengetahui beberapa faktor yang dapat memengaruhi tekuk pada kolom. Namun, masalah utama dari tekuk adalah ketidakstabilan geometris. Kolom pada kenyataannya kolom tidak pernah memiliki bentuk sempurna, pasti ada kecacatan meskipun sangat kecil. Begitu pula dengan pembebanan, tidak ada pembebanan yang sempurna berada di pusat sumbu kolom. Meskipun terlihat remeh, hal ini dapat memperbesar kemungkinan terjadi tekuk. Oleh karena itu, dilakukan analisis matematis dalam mendesain kolom untuk mengetahui batas beban yang dapat diterima sehingga tekuk dapat dihindari.
Jika kamu tertarik mempelajari lebih dalam mengenai struktur baja, beton, geoteknik, konstruksi, hidrologi, dan teknologi material ramah lingkungan, Program Studi Teknik Sipil Universitas Internasional Batam (UIB) adalah tempat terbaik untuk mengembangkan diri kamu.
Editor: Ade Jaya Saputra, S.T., M.Eng.